Можно ли считать что нулевой вектор может быть коллинеарен любому вектору
Содержание статьи
Условие коллинеарности векторов, когда векторы параллельны, свойства коллинеарных векторов
В статье ниже рассмотрим условия, при которых векторы считаются коллинеарными, а также разберем тему на конкретных примерах. И, прежде чем приступить к обсуждению, напомним некоторые определения.
Определение 1
Коллинеарные векторы – ненулевые векторы, лежащие на одной прямой или на параллельных прямых. Нулевой вектор считается коллинеарным любому другому.
Данное определение дает возможность убедиться в коллинеарности векторов в их геометрическом отображении, однако точность такого способа может иметь погрешности, например, в зависимости, от качества самого чертежа. Поэтому обратимся к алгебраическому толкованию: сформируем условие, которое будет явным признаком коллинеарности.
Согласно схемам операций над векторами умножение вектора на некоторое заданное число приводит к соответствующему сжатию или растяжению вектора при сохранении или смене направления. Тогда вектор b→=λ·a→ коллинеарен вектору a→ , где λ – некоторое действительное число. Справедливым будет и обратное утверждение: если вектор b→ коллинеарен вектору a→, его можно представить в виде λ·a→. Это является необходимым и достаточным условием коллинеарности двух ненулевых векторов.
Определение 2
Для коллинеарности двух векторов необходимо и достаточно, чтобы они были связаны равенствами: b→=λ·a→ или a→=μ·b→, μ∈R
Координатная форма условия коллинеарности векторов
Исходные данные: вектор a→ задан в некоторой прямоугольной системе координат на плоскости и имеет координаты (ax, ay), тогда, согласно полученному выше условию, вектор b→=λ·a→ имеет координаты (λ·ax, λ·ay).
По аналогии: если вектор a→ задан в трехмерном пространстве, то он будет представлен в виде координат a=(ax, ay, az) , а вектор b→=λ·a→ имеет координаты (λ·ax, λ·ay, λ·az). Из полученных утверждений следуют условия коллинеарности двух векторов в координатном толковании.
Определение 3
- Для коллинеарности двух ненулевых векторов на плоскости необходимо и достаточно, чтобы их координаты были связаны соотношениями: bx=λ·axby=λ·ay или ax=μ·bxay=μ·by
- Для коллинеарности двух ненулевых векторов в пространстве необходимо и достаточно, чтобы их координаты были связаны соотношениями:bx=λ·axby=λ·ay bz=λ·azили ax=μ·bxay=μ·by az=μ·bz
Мы можем также получить еще одно условие коллинеарности векторов, опираясь на понятие их произведения.
Если ненулевые векторы a→=(ax, ay, az) и b→=(bx, by, bz) коллинеарны, то согласно векторному определению произведения a→×b→=0→. И это также соответствует равенству: i→j→k→axayazbxbybz=0→, что, в свою очередь, возможно только тогда, когда заданные векторы связаны соотношениями b→=λ·a→ и a→=μ·b→ , где μ — произвольное действительное число (на основании теоремы о ранге матрицы), что указывает на факт коллинеарности векторов.
Определение 4
Два ненулевых вектора коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору.
Рассмотрим применение условия коллинеарности на конкретных примерах.
Пример 1
Исходные данные: векторы a→=(3-22, 1) и b→=(12+1, 2+1) . Необходимо определить, коллинеарны ли они.
Решение
Выполним задачу, опираясь на условие коллинеарности векторов на плоскости в координатах: bx=λ·axby=λ·ay Подставив заданные значения координат, получим: bx=λ·ax⇔12+1=λ·(3-22)⇒λ=1(2+1)·(3-22)=132-4+3-22=12-1by=λ·ay⇔2+1=12-1·1⇔(2+1)·(2-1)=1 ⇔1≡1
Т.е. b→=12-1·a→, следовательно, заданные векторы коллинеарны.
Ответ: заданные векторы коллинеарны.
Пример 2
Исходные данные: векторы a→=(1, 0, -2) и b→=(-3, 0, 6) . Необходимо убедиться в их коллинеарности.
Решение
Т.к. bx=λ·axby=λ·ay bz=λ·az⇔-3=-3·10=-3·06=-3·(-2) , то верным будет равенство: b→=-3·a→ , что является необходимым и достаточным условием коллинеарности. Таким образом, заданные векторы коллинеарны.
Найдем также векторное произведение заданных векторов и убедимся, что оно равно нулевому вектору: a→×b→=i→j→k→axayazbxbybz=i→j→k→10-2-306=i→·0·6+j→·(-2)·(-3)+k→·1·0-k→·0·(-3)-j→·1·6-i→·(-2)·0=0→Ответ: заданные векторы коллинеарны.
Пример 3
Исходные данные: векторы a→=(2, 7) и b→=(p, 3) . Необходимо определить, при каком значении pзаданные векторы будут коллинеарны.
Решение
Согласно выведенному выше условию, векторы коллинеарны, если
b→=λ·a→⇔bx=λ·axby=λ·ay⇔p=λ·23=λ·7
тогда λ=37, а p=λ·2⇔p=67 .
Ответ: при p=67 заданные векторы коллинеарны.
Также распространены задачи на нахождения вектора, коллинеарного заданному. Решаются они без затруднений, основываясь на условии коллинеарности: : достаточным будет взять произвольное действительное число λ и определить вектор, коллинеарный данному.
Пример 4
Исходные данные: вектор a→=(2, -6) . Необходимо найти любой ненулевой вектор, коллинеарный заданному.
Решение
Ответом может послужить, например, 12·a→=(1, -3) или вектор 3·a→=(6, -18) .
Ответ: вектор, коллинеарный заданному имеет координаты (1, -3).
Пример 5
Исходные данные: вектор a→=(3, 4, -5) . Необходимо определить координаты вектора единичной длины, коллинеарного заданному.
Решение
Вычислим длину заданного вектора по его координатам: a→=ax2+bx2+cx2=32+42+(-5)2=52 Разделим каждую из заданных координат на полученную длину и получим единичный вектор, коллинеарный данному: 1a→·a→=(352, 452,- 12)
Ответ: (352, 452,- 12)
Источник
Нулевой вектор коллинеарен любому вектору.
Равными называются два сонаправленных вектора, имеющих равные модули. Равные векторы также называют свободными.
Два вектора, равные третьему вектору, равны.
Вектор можно перемещать вдоль прямой, совпадающей с его направлением и переносить его параллельно самому себе в любую точку пространства.
D С
A В ↑↑
| |=| | =
В параллелепипеде АВСDА1В1С1 D1 изобразить векторы: сонаправленные, противоположно направленные, равные.
три группы коллинеарных,сонаправленных
D1 C1 векторов: . . .
А1 В1 = — равные векторы
D C
А В
D1 C1 Векторы ;
коллинеарны е, противоположно направленные
А1 В1
D С
Компланарными называются три вектора, если при откладывании их от одной точки они лежат в одной плоскости.
Любые два вектора — компланарные.
Три вектора, два из которых коллинеарные, — компланарные.
В1 С1Векторыкомпланарные
А1 D1
В С
А D
КООРДИНАТЫ ВЕКТОРА
Координаты точки – это числа, соответствующиеее проекциям на оси координат. Проекциями произвольного отрезка на оси координат являются проекции этого отрезка на оси координат.
Для вектора , имеющего начало в точке О(0;0), координаты точки А являются
координатами вектора. Записывается: { хА; уА }. Такая запись называется: «Запись вектора в координатной форме». Пусть А(3;2), тогда { 3;2 }.
При выполнении действий с векторами единицы масштаба
у называют координатными векторами(ортами) и обозначают: по оси
абсцисс, и по оси ординат и по оси аппликат.
В нашем случае = 3 =2 (на плоскости)
проекция вектора на ось 0х равна 3 ; на ось 0у равна 2 .
уА А (3;2)
И по правилу сложения векторов = х +у .
Такая запись называется: «Разложение вектора по ортам»
в нашем случае = 3 +2 .
хА х
Если начало вектора не совпадает с началом координат, то координатами вектора являются его проекции на оси координат: (хВ– хА , уВ– уА). И тогда в координатной форме вектор записывается: { (хВ–хА); (уВ–уА) }. В нашем случае: А(1;3), В (4;5), и в координатной форме вектор записывается: { 3; 2 }, а егоразложение по ортам: = 3 + 2 .
у
уВ В (4;5) В прямоугольном треугольнике АСВ: катеты АС и ВС,
гипотенуза — вектор { 3; 2 }, и по теореме Пифагора
у длина вектора, или его модуль вычисляется по формуле
| | = , (1)если
уА А(1;3) С заданы координаты точек А и В;
или | | = , (2)если
векторзадан в координатной форме или в виде
0 хА х хВ х разложения по ортам.
Если 0х, то проекции точек А и В совпадают и проекция вектора ось 0х равна
у z Для трехмерного пространства
пр.Оz
пр.Оу
0у
Х
На плоскости пр.Ох = 0
х
Для трехмерного пространства во всех формулах добавляется третья координата:
{ (хВ–хА); (уВ–уА);(zB — zA)},
= x + y +z
| | = .
Проекция вектора на ось равна произведению модуля вектора на косинус угла между вектором и осью: пр.Ох = | | ·cos .
Проекция вектора на ось положительное число (+),если
направление вектора совпадает с положительным направлением оси,
х т.е. = пр.Ох = | | ·cos .
Проекция вектора на ось отрицательное число (–),если
вектор и ось имеют противоположные направления.
или если < < π пр.Ох = — | | ·cos .
х
1.Проекции равных векторов на одну и ту же ось равны.
2. В данной системе координат каждый вектор имеет единственный набор координат.
3. Координаты вектора, отложенного от произвольной точки, равны разности
соответствующих координат его конца и начала.
4.Векторы параллельны (коллинеарные) тогда и только тогда, когда их координаты
пропорциональны
1.Записать координаты вектора: = 4 + 5 + 3 z
= 4 + 5 +3 { 4; 5; 3}
Графически это означает: 3
А (4;5; 3)
0 5 у
4
х А1(4;5)
2. Записать координаты векторов:
= – 4 + – { –4; 1; –1 }
= – 2 + { 0; – 2; 1 } ; = + { 0; 1; 1}
= – {–1; 0; 1 }; = 0,7 { 0; 0; 0,7}
3. Если вектор отложен от начала координат, то координаты вектора равны координатам конца вектора. Векторы 1 ; 1; 1; 1в этом случае называются радиус-векторами.
Упрямоугольного параллелепипеда ОА = 2, ОС = 3, ОО1 = 2.
Найдите координаты векторов 1 ; 1; 1; ; ; ;
z
O1 А1 (2; 0; 2) 1 { 2; 0;2 } 1 = 2 + 2 ,
С1
A1 В1
2
O 3 С В1 ( 2; 3; 2) 1 { 2; 3; 2} 1 = 2 + 3 + 2
2 у
х A BО1( 0; 0; 2) 1 { 0; 0; 2} 1 = 2 ,
С1(0,3;2); О1(0,0;2); А(2,0;0); С(0,3;0); В( 2; 3; 0)
{ — 2,3; 2 } ; {— 2, 0; 2 } ; { 0; 3; -2}
4.Найти длину радиус- векторов , , , если А(0,2;5); В(-1; 3; ); С(3; -2; 2 ).
| | = = =
| | = = = 4
| | = = = 5
5.Даны две координаты вектора {4; -12; z} . Найти его третью координату, если:| | =13
| | = 132 = 16 + 144 +z2 z2 = 9 z = ± 3
6. Какие координаты имеет вектор , если А(1;2;3): = + 2 + 3
А(-5;4;-1): = -5 + 4 —
7. Назовите координаты векторов: а) =– 2 + 6 ={ – 2; 6 }
б) = + 3 { 1; 3} в) = – 3 { 0;– 3} d) = – 5 { –5; 0}
8. Разложите по координатным векторам , если А(0;0;2) и С(0;2;0)
= 0 + 2 –2 , = 2 –2
8. Даны точки А(2; –3: 0); В(7; –12; 18); С (–8; 0; 5). Записать координаты векторов
; ; { 2; –3: 0} { 7; –12; 18 } { –8; 0; 5}
Письменно ответьте на вопросы
- Что называется вектором?
- Что называется модулем вектора?
- Какие векторы называются нулевыми? Равными?
- Какие векторы называются коллинеарными? Компланарными?
- Что называется координатами вектора?
- В каком случае координата вектора равна нулю?
- Сформулируйте признак коллинеарности векторов.
- В каком случае все три координаты вектора равны нулю?
- Что называется разложением вектора по координатным векторам?
- Что означают числа х, у, z при записи вектора в координатной форме?
- Какова связь между проекцией вектора на ось, модулем вектора и углом между вектором и координатной осью?
Выполните задания:
1.Даны векторы { 3; 2; 1} ; { 1; –3; 5 } ; { – ; 0,75; –2 } . Запишите координаты точек А(2; –3: 0); В(7; –12; 18); С (–8; 0; 5).
2. Запишите в координатной форме ВС, если С(-2; 1; 3); В(3; -2; 1)
3. Вершины куба имеют координаты А(3;-1;1); В(-1;-1;1); С(-1; 3; 1); С1 (-1; 3; 5).
а) найдите координаты вершин В1и D1
б) разложите по координатным векторам векторы:и
4. Векторы иравны. Найдите координаты точки А, если { – 1; 2; 4 } и С(2;0;5)
5. Определить, при каких значениях т векторы иравны, если { 2т; 2 } и {т; 1}.
6. Найдите значения т и п, при которых векторы иудут коллинеарными, если { 1; – 2; т },
{ п; 6; 3 }.
7. Векторы { 10; т; 5 } и { п; 3; 2} коллинеарные. Найти значения т и п .
8.Даны точки А(2; –3: 0); В(7; –12; 18); С (–8; 0; 5). Записать координаты векторов
; ;
9. Найти координаты вершины D параллелограмма АВСD, если А(3; 0; 1); В(4; 2; –1); С (1; 2; 5);
10. Проверить, являются ли точки А(– 4; – 4); В(–3; 4); С (4; 5); D(10; –2) вершинами трапеции
АВСD.
СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ. УМНОЖЕНИЕ ВЕКТОРА НА
ЧИСЛО.
Векторная алгебра — раздел математики, изучающий векторы. Векторная алгебра является одним из основных средств исследования в физике и разных разделах математики. В векторной форме записываются многие законы физики и механики, И в геометрии аппарат векторов позволяет кратко записывать формулировки задач и их решения, например, теорема о средней линии треугольника в векторной форме записывается так
А , а доказывается в одну строку:
К L
В С
Чтобы объединить преимущества координатного и векторного методов, для векторов введены координаты. Это позволяет свести действия с векторами к аналогичным действиям с их координатами, и проводить действия с векторами так, как это делается в обычной алгебре: слагаемые менять местами, вводить скобки, группировать, выносить за скобки как скалярные, так и векторные множители.
Источник
Урок по теме «Векторы в пространстве»
Цели урока:
- Обучающая:понятие вектора в курсе
планиметрии; изучить векторы в пространстве;
определить основные понятия для векторов:
направление вектора, абсолютная величина,
равенство векторов, нулевой вектор; закрепить
новые понятия на практических задачах. - Развивающая:показать учащимся широкий
спектр возможностей применения векторов;
развивать стремление к достижению поставленной
цели, способность переноса ЗУН на новые ситуации;
совершенствовать пространственное воображение
и мышление учащихся; развивать навыки диалоговой
культуры. - Воспитывающая: воспитать математическую
культуру, грамотность; формировать активность,
внимательность, наблюдательность.
Тип урока: обобщение и систематизация знаний.
Метод обучения:
объяснительно-иллюстративный в форме беседы,
частично-поисковый.
Оборудование к уроку:компьютер, экран,
таблица “Векторы в пространстве”,презентация
“Векторы в пространстве”.
Литература:
- Глейзер Г.И. “История математики в школе: 9-10
кл.” . - Ершова А.П., Голобородько В.В. “Устные
проверочные и зачетные работы по геометрии 10-11
класс”. - Журнал “Математика в школе”, N94 1990, № 4 1994, №5 1995,
№3 1996. - Малова И.Е. и др. “Методика обучения учащихся
математики”. - Погорелов А.В. Геометрия: Учебник для 7-11 классов
средней школы.
План урока:
- Организационный этап (подготовительный).
- Сообщение темы и целей урока.
- Актуализация знаний.
- Обобщение и систематизация знаний по теме.
- Закрепление полученных знаний.
- Постановка домашнего задания.
- Подведение итогов.
Ход урока
Организационный этап (подготовительный).
Приветствие учащихся, проверка отсутствующих,
а также готовность учащихся к уроку.
Сообщение темы и целей урока.
— Ребята, тема сегодняшнего урока “Векторы в
пространстве”(слайд 1).
Мы с вами должны вспомнить понятие вектора на
плоскости и перенести полученные ЗУН на
рассмотрение векторов в пространстве, а также
определить основные понятия для векторов и
заполнить таблицу “Векторы в пространстве,
которую вы получили перед началом урока вот
таком виде (слайд 2).
| Название определения | Формулировка определения | Запись |
| Вектор | ||
| Нулевой вектор | ||
| Одинаково-направленные (сонаправленные) | ||
| Противоположно-направленные | ||
| Коллинеарные векторы | ||
| Абсолютная величина | ||
| Равные векторы |
3. Актуализация знаний.
— С понятием “вектор” вам приходилось
встречаться очень часто. Где?
физике (направление силы, скорости,
ускорения и др.)
пример: Для того, чтобы охарактеризовать
движение тела в данный момент, недостаточно
сказать, что оно движется с какой-то скоростью,
надо указать направление его движения. (слайд 3)
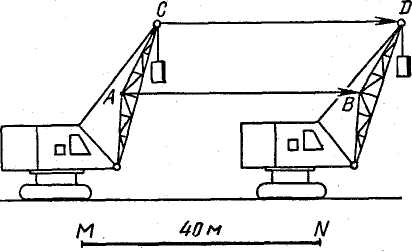
— Исходя из данного примера физики, каким
образом вы определяли понятие вектора на
плоскости?
Учащиеся: Вектор – это направленный
отрезок.
— На сегодняшний день, кроме как в физике и
геометрии курса планиметриигде вы сталкивались
с вектором?
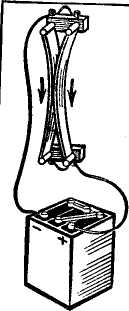
электротехнике (направление
электрического тока, магнитной индукции,
магнитного потока и т.д.)
— Какие можно назвать векторные величины в
пространстве?
Пример: движение заряженных частиц в
магнитном поле, которое характеризуется в каждой
точке пространства вектором магнитной индукции В.(слайд
4)
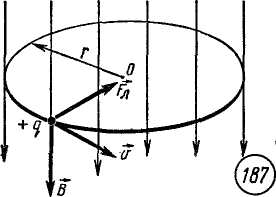
Обобщение и систематизация знаний по теме.
— Как вы думаете, на основе данного примера, что
можно сказать о векторе в пространстве? Что такое
вектор?
Учащиеся: Вектор – это направленный
отрезок. (слайд 5)
— Каким образом изображается вектор на рисунке?
Учащиеся: Стрелкой. (слайд 6)
— Обозначается?
Учащиеся: Либо большими, либо прописными
латинскими буквами. (слайд 6)
— Давайте занесем это в таблицу.
| Название определения | Формулировка определения | Запись |
| Вектор | направленный отрезок |
— Хорошо, мы с вами определили понятие вектора.
Далее мы должны рассмотреть основные понятия
векторов в пространстве: направление вектора,
абсолютная величина, равенство векторов.
— Но прежде чем рассмотреть данные понятия
ответьте на такой вопрос. Как называется вектор,
у которого начало совпадает с концом?
(Выслушиваются мнения учащихся).
— Итак, вектор у которого начало совпадает с
концом вектора называется нулевым. (слайд 7)
Обозначение:
Изображение: в виде точки.
— Занесем данные в таблицу
| Название определения | Формулировка определения | Запись |
| нулевой вектор | вектор, у которого начало совпадает с концом |
— Далее перейдем к рассмотрению направления
векторов. Итак, вектор-это направленный отрезок,
а если у нас имеется два вектора, как могут быть
направлены эти векторы? (Выслушиваются мнения
учащихся).
— Итак, вспомнили, два вектора, могут быть
одинаково- направленными (сонаправленными) и
противоположно- направленными. (слайд 8)
— В пространстве также два вектора могут быть
одинаково-направленными (сонапрвленными) и
противоположно-направленными.
Пример:
Следовательно, одинаково-направленные
(сонаправленные) векторыимеют одно
направление, а противоположно-направленные
– противоположное направление.(слайд 9)
Запись: в виде стрелок.(слайд 9).
— Отметим это в таблице.
— Далее рассмотрим устно задачу.(слайд10)
Задача. На рисунке определите
одинаково-направленные (сонаправленные) и
противоположно-направленные векторы.
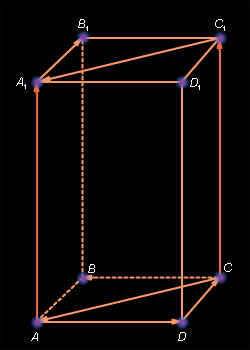
Решение:
одинаково-направленные
противоположно-направленные
Игровой вопрос.
— Ответьте как называются ненулевые векторы,
которые лежат на одной прямой или на
параллельных прямых?
Учащиеся: коллинеарные
— Итак, коллинеарные векторы- это
ненулевые векторы, которые лежат на одной прямой
или на параллельных прямых.
— Запишем в таблицу определение коллинеарных
векторов.
| Название определения | Формулировка определения | Запись |
| коллинеарные векторы | это ненулевые векторы, которые лежат на одной прямой или на параллельных прямых | одинаково-направ. противоположно-направ. |
Коллинеарные векторы могут быть
одинаково-направленными (сонаправленными) и
противоположно-направленными. (слайд 11)
Запись: и
— Итак, с одним основным понятием векторов мы
познакомились. Далее вспомним абсолютную
величину (или модуль) вектора. Что такое
абсолютная величина вектора, вспоминаем.
(Выслушиваются мнения учащихся).
Учащиеся: — это длина отрезка, изображающего
вектор.
— Посмотрим определение абсолютной величины
вектора в пространстве.(слайд 12)
— Что мы видим отличий нет.
Абсолютная величина (модуль)– это длина
отрезка, изображающего вектор.
Запись:
— Занесем данное понятие в таблицу.
| Название определения | Формулировка определения | Запись |
| абсолютная величина (модуль) | длина отрезка, изображающего вектор |
— Как находится абсолютная величина вектора мы
рассмотрим на следующем уроке, когда
познакомимся с координатами вектора.
— И перейдем к последнему понятию связанному с
вектором — это равные векторы. Итак, какие векторы
называются равными? (Выслушиваются мнения
учащихся)
(слайд 13)
Равные векторы – это векторы, которые
одинаково направлены (сонаправленные ) и имеют
равные длины.
Запись:
— Занесем в таблицу определение равных векторов
, а также запись равных векторов.
| Название определения | Формулировка определения | Запись |
| равные векторы | векторы, которые сонаправлены и имеют равные длины |
— Итак, мы рассмотрели с вами определение
вектора в пространстве и все понятия, связанные с
ним. Заполнили таблицу, которая вам поможет в
дальнейшем при изучении темы и при выполнении
домашнего задания:
5. Закрепление полученных знаний
Задание 2
Выберите один из вариантов ответа “да” или
“нет” на следующие вопросы:
1.Можно ли считать, что нулевой вектор может
быть коллинеарен любому вектору? (да)
2.Два вектора, сонаправленные с ненулевым
вектором, сонаправленны? (да)
3. Верно ли, что векторы и
противоположно-направленные? (да)
4. Два вектора, коллинеарные ненулевому вектору,
сонаправлены? (нет)
5. Справедливо ли утверждение: Любые два
сонаправленных вектора равны? (нет)
6. Согласны ли вы, что любые два
противоположно-направленных вектора
коллинеарны? (нет)
7. Верно ли, что любые два равных ненулевых
вектора коллинеарны? (нет )
Домашнее задание
- параграф 4, п.35 с.54.
- таблица, сделанная на уроке.
- прочитать п.36, разобрать задачи в этом пункте.
Подведение итогов
— Итак, мы с вами изучили тему “Векторы в
пространстве”.
Вопросы:
- Что нового узнали из этой темы?
- Назовите основные понятия, связанные с
вектором.
Выставить оценки с комментарием, отметить
наиболее отличившихся учащихся.
Источник